Các số nguyên tố đã thu hút sự chú ý của con người từ những ngày đầu của nền văn minh. Chúng tôi giải thích họ là gì, tại sao nghiên cứu của họ lại kích thích các nhà toán học và nghiệp dư như nhau, và trên con đường chúng tôi mở ra một cánh cửa vào thế giới của các nhà toán học.
Từ thuở sơ khai của lịch sử loài người, số nguyên tố đã khơi dậy trí tò mò của con người. Họ là ai? Tại sao những câu hỏi liên quan đến chúng lại khó đến vậy? Một trong những điều thú vị nhất về số nguyên tố là sự phân bố của chúng giữa các số tự nhiên. Ở quy mô nhỏ, sự xuất hiện của các số nguyên tố có vẻ ngẫu nhiên, nhưng ở quy mô lớn lại xuất hiện một kiểu mẫu, điều này vẫn chưa được hiểu đầy đủ. Trong bài báo ngắn này, chúng tôi sẽ cố gắng theo dõi lịch sử của các số nguyên tố từ thời cổ đại và sử dụng cơ hội này để đi sâu vào và hiểu rõ hơn về thế giới của các nhà toán học.
SỐ TỔNG HỢP VÀ SỐ NGUYÊN TỐ
Bạn đã bao giờ tự hỏi tại sao ngày được chia thành 24 h và vòng tròn thành 360 độ? Con số 24 có một tính chất thú vị: nó có thể được chia thành các phần bằng nhau theo một số lượng tương đối lớn. Ví dụ: 24 ÷ 2 = 12, 24 ÷ 3 = 8, 24 ÷ 4 = 6, v.v. (tự hoàn thành các tùy chọn còn lại!). Điều này có nghĩa là một ngày có thể được chia thành hai phần bằng nhau, mỗi phần 12 giờ, ban ngày và ban đêm. Trong một nhà máy làm việc không ngừng theo ca 8 tiếng, mỗi ngày được chia đúng ba ca.
Đây cũng là lý do tại sao vòng tròn được chia thành 360 °. Nếu hình tròn được chia thành hai, ba, bốn, mười, mười hai hoặc ba mươi phần bằng nhau, thì mỗi phần sẽ chứa một số nguyên; và có những cách chia vòng tròn bổ sung mà chúng tôi không đề cập đến. Vào thời cổ đại, việc chia một vòng tròn thành các phần có kích thước bằng nhau với độ chính xác cao là cần thiết cho các mục đích nghệ thuật, thiên văn và kỹ thuật khác nhau. Với la bàn và thước đo góc là những công cụ duy nhất hiện có, việc chia một hình tròn thành các phần bằng nhau có giá trị thực tiễn rất lớn. 1
Một số nguyên có thể viết được dưới dạng tích của hai số nhỏ hơn được gọi là hợp số
. Ví dụ, phương trình 24 = 4 × 6 và 33 = 3 × 11 cho thấy 24 và 33 là các số hợp. Một số không thể chia nhỏ theo cách này được gọi là số nguyên tố
. Những con số
2, 3, 5, 7, 11, 13, 17, 19, 23 và 29
đều là số nguyên tố. Trên thực tế, đây là 10 số nguyên tố đầu tiên (bạn có thể tự kiểm tra điều này nếu muốn!).
Nhìn vào danh sách ngắn các số nguyên tố này có thể tiết lộ một vài quan sát thú vị. Đầu tiên, ngoại trừ số 2, tất cả các số nguyên tố đều là số lẻ, vì một số chẵn chia hết cho 2 nên nó là hợp số. Vì vậy, khoảng cách giữa hai số nguyên tố bất kỳ trong một hàng (gọi là liên tiếpsố nguyên tố) ít nhất là 2. Trong danh sách của chúng tôi, chúng tôi tìm thấy các số nguyên tố liên tiếp có hiệu của chúng chính xác là 2 (chẳng hạn như các cặp 3,5 và 17,19). Cũng có những khoảng cách lớn hơn giữa các số nguyên tố liên tiếp, như khoảng cách sáu số giữa 23 và 29; mỗi số 24, 25, 26, 27 và 28 là một số tổng hợp. Một quan sát thú vị khác là trong mỗi nhóm thứ nhất và thứ hai của 10 số (có nghĩa là từ 1–10 đến 11–20) có bốn số nguyên tố, nhưng trong nhóm thứ ba của 10 (21–30) chỉ có hai. Điều đó có nghĩa là gì? Các số nguyên tố có trở nên hiếm hơn khi các số lớn lên không? Có ai có thể hứa với chúng tôi rằng chúng tôi sẽ có thể tiếp tục tìm được nhiều số nguyên tố hơn và vô thời hạn không?
Nếu ở giai đoạn này, có điều gì đó kích thích bạn và bạn muốn tiếp tục điều tra danh sách các số nguyên tố và các câu hỏi mà chúng tôi nêu ra, điều này có nghĩa là bạn có tâm hồn của một nhà toán học. Dừng lại! Đừng đọc tiếp! 2 Lấy một cây bút chì và một mảnh giấy. Viết tất cả các số có đến 100 và đánh dấu các số nguyên tố. Kiểm tra xem có bao nhiêu cặp có hiệu số là hai. Kiểm tra xem có bao nhiêu số nguyên tố trong mỗi nhóm 10. Bạn có thể tìm thấy bất kỳ mẫu nào? Hay danh sách các số nguyên tố lên đến 100 có vẻ ngẫu nhiên đối với bạn?
MỘT SỐ LỊCH SỬ VÀ KHÁI NIỆM CỦA MỘT ĐỊNH LÝ
Số nguyên tố đã chiếm sự chú ý của con người từ thời cổ đại và thậm chí còn được liên kết với siêu nhiên. Ngay cả ngày nay, trong thời hiện đại, có những người cố gắng cung cấp các số nguyên tố với các tính chất thần bí . Nhà thiên văn học và tác giả khoa học nổi tiếng Carl Sagan đã viết một cuốn sách vào năm 1985 có tên “Liên hệ”, đề cập đến việc người ngoài Trái đất (một nền văn hóa giống người bên ngoài trái đất) cố gắng giao tiếp với con người bằng cách sử dụng các số nguyên tố làm tín hiệu. Ý tưởng rằng các tín hiệu dựa trên các số nguyên tố có thể làm cơ sở để giao tiếp với các nền văn hóa ngoài Trái đất vẫn tiếp tục khơi dậy trí tưởng tượng của nhiều người cho đến ngày nay.
Người ta thường cho rằng sự quan tâm nghiêm túc đến các số nguyên tố bắt đầu từ thời Pythagoras. Pythagoras là một nhà toán học Hy Lạp cổ đại. Các học trò của ông, những người theo thuyết Pitago – một phần là nhà khoa học và một phần là nhà thần bí – sống vào thế kỷ thứ sáu trước Công nguyên. Họ không để lại bằng chứng bằng văn bản và những gì chúng ta biết về họ đến từ những câu chuyện được truyền miệng. Ba trăm năm sau, vào thế kỷ thứ ba trước Công nguyên, Alexandria (thuộc Ai Cập hiện đại) là thủ đô văn hóa của thế giới Hy Lạp. Euclid ( Hình 1), người sống ở Alexandria trong thời Ptolemy đầu tiên, có thể được bạn biết đến từ hình học Euclide, được đặt theo tên của ông. Hình học Euclid đã được giảng dạy trong các trường học trong hơn 2.000 năm. Nhưng Euclid cũng quan tâm đến các con số. Trong cuốn sách thứ chín của tác phẩm “Các yếu tố”, trong Mệnh đề 20, lần đầu tiên xuất hiện một bằng chứng toán học
của định lý
rằng có vô hạn số nguyên tố.

- Hình 1
- Những người đứng sau các số nguyên tố.
Đây là một nơi tốt để nói một vài lời về các khái niệm của định lý và chứng minh toán học. Một định lýlà một câu lệnh được diễn đạt bằng ngôn ngữ toán học và có thể nói một cách chắc chắn là hợp lệ hoặc không hợp lệ. Ví dụ, định lý “có vô số số nguyên tố” tuyên bố rằng trong hệ thống các số tự nhiên (1,2,3…) danh sách các số nguyên tố là vô tận. Nói chính xác hơn, định lý này tuyên bố rằng nếu chúng ta viết một danh sách hữu hạn các số nguyên tố, chúng ta sẽ luôn có thể tìm thấy một số nguyên tố khác không có trong danh sách đó. Để chứng minh định lý này, chỉ ra một số nguyên tố bổ sung cho một danh sách cụ thể là không đủ. Ví dụ: nếu chúng ta chỉ ra 31 là một số nguyên tố nằm ngoài danh sách 10 số nguyên tố đầu tiên được đề cập trước đó, chúng ta thực sự sẽ thấy rằng danh sách đó không bao gồm tất cả các số nguyên tố. Nhưng có lẽ bằng cách thêm 31, bây giờ chúng ta đã tìm thấy tất cả các số nguyên tố, và không còn nữa? Những gì chúng ta cần làm,bất kỳ danh sách hữu hạn nào , miễn là nó có thể có, chúng ta có thể tìm thấy một số nguyên tố không có trong nó. Trong phần tiếp theo, chúng tôi sẽ trình bày bằng chứng của Euclid mà không làm bạn quá nhiều chi tiết.
CHỨNG MINH CỦA EUCLID VỀ SỰ TỒN TẠI CỦA VÔ SỐ SỐ NGUYÊN TỐ
Để chứng minh rằng có vô hạn số nguyên tố, Euclid đã sử dụng một định lý cơ bản khác mà ông đã biết, đó là phát biểu rằng “ mọi số tự nhiên có thể được viết dưới dạng tích của các số nguyên tố. ” Rất dễ bị thuyết phục về sự thật của tuyên bố cuối cùng này. Nếu bạn chọn một số không phải là hỗn hợp, thì số đó chính là số nguyên tố. Nếu không, bạn có thể viết số bạn đã chọn dưới dạng tích của hai số nhỏ hơn. Nếu mỗi số nhỏ hơn là số nguyên tố, bạn đã biểu thị số của mình dưới dạng tích các số nguyên tố. Nếu không, hãy viết các số tổng hợp nhỏ hơn dưới dạng tích của các số vẫn nhỏ hơn, v.v. Trong quá trình này, bạn tiếp tục thay thế bất kỳ số tổng hợp nào bằng các sản phẩm có số nhỏ hơn. Vì không thể làm điều này mãi mãi, quá trình này phải kết thúc và tất cả các số nhỏ hơn mà bạn kết thúc không thể chia nhỏ được nữa, có nghĩa là chúng là số nguyên tố. Ví dụ, chúng ta hãy chia nhỏ số 72 thành các thừa số nguyên tố của nó:
72 = 12 × 6 = 3 × 4 × 6 = 3 × 2 × 2 × 6 = 3 × 2 × 2 × 2 × 3.
Dựa trên thực tế cơ bản này, bây giờ chúng ta có thể giải thích bằng chứng tuyệt vời của Euclid cho tính vô hạn của tập hợp các số nguyên tố. Chúng tôi sẽ chứng minh ý tưởng bằng cách sử dụng danh sách 10 số nguyên tố đầu tiên nhưng lưu ý rằng ý tưởng tương tự này hoạt động cho bất kỳ danh sách hữu hạn các số nguyên tố nào. Hãy nhân tất cả các số trong danh sách và thêm một vào kết quả. Cho tên N vào số ta được. (Giá trị của N không thực sự quan trọng vì đối số phải hợp lệ với bất kỳ danh sách nào.)
N = (2 × 3 × 5 × 7 × 11 × 13 × 17 × 19 × 23 × 29) +1.
Số N , cũng giống như bất kỳ số tự nhiên nào khác, có thể được viết dưới dạng tích các số nguyên tố. Những số nguyên tố, thừa số nguyên tố của N là ai? Chúng tôi không biết, bởi vì chúng tôi đã không tính họ, nhưng có một điều chúng ta biết chắc chắn là: tất cả họ đều chia N . Nhưng số N để lại phần dư là một khi chia cho bất kỳ số nguyên tố nào trong danh sách của chúng ta 2, 3, 5, 7,…, 23, 29. Đây được cho là một danh sách đầy đủ các số nguyên tố của chúng ta, nhưng không có số nào trong số chúng chia N . Vì vậy, các thừa số nguyên tố của N không nằm trong danh sách đó và đặc biệt phải có các số nguyên tố mới vượt quá 29.
RÂY CỦA ERATOSTHENES
Bạn đã tìm thấy tất cả các số nguyên tố nhỏ hơn 100 chưa? Bạn đã sử dụng phương pháp nào? Bạn đã kiểm tra từng số riêng lẻ, để xem nó có chia hết cho các số nhỏ hơn không? Nếu đây là cách bạn đã chọn, bạn chắc chắn đã đầu tư rất nhiều thời gian. Eratosthenes ( Hình 1 ), một trong những học giả vĩ đại nhất của thời kỳ Hy Lạp hóa, sống sau Euclid vài thập kỷ. Ông từng là thủ thư trưởng của thư viện Alexandria, thư viện đầu tiên trong lịch sử và lớn nhất thế giới cổ đại. Ông không chỉ quan tâm đến toán học mà còn quan tâm đến thiên văn, âm nhạc và địa lý, và là người đầu tiên tính toán chu vi trái đất với độ chính xác ấn tượng vào thời đại của mình. Trong số những thứ khác, ông đã thiết kế một cách thông minh để tìm tất cả các số nguyên tố cho đến một số nhất định. Vì phương pháp này dựa trên ý tưởng sàng (sàng) các số tổng hợp, nó được gọi là Sieve of Eratosthenes .
Chúng tôi sẽ chứng minh sàng của Eratosthenes trong danh sách các số nguyên tố nhỏ hơn 100, hy vọng vẫn còn ở phía trước của bạn ( Hình 2). Khoanh tròn số 2, vì nó là số nguyên tố đầu tiên, rồi xóa tất cả các bội số cao hơn của nó, cụ thể là tất cả các số chẵn tổng hợp. Chuyển sang số không bị xóa tiếp theo, số 3. Vì nó không bị xóa nên nó không phải là tích của các số nhỏ hơn, và chúng ta có thể khoanh tròn nó khi biết rằng nó là số nguyên tố. Một lần nữa, xóa tất cả các bội số cao hơn của nó. Lưu ý rằng một số trong số họ, chẳng hạn như 6, đã bị xóa, trong khi những người khác, chẳng hạn như 9, sẽ bị xóa ngay bây giờ. Số tiếp theo không bị xóa — 5 — sẽ được khoanh tròn. Một lần nữa, hãy xóa tất cả các bội số cao hơn của nó: 10, 15 và 20 đã bị xóa, nhưng 25 và 35 chẳng hạn, sẽ bị xóa ngay bây giờ. Tiếp tục theo cách tương tự. Cho đến khi? Hãy thử nghĩ tại sao sau khi vượt qua10=100chúng ta không cần phải tiếp tục quá trình. Tất cả các số nhỏ hơn 100 không bị xóa đều là số nguyên tố và có thể được khoanh tròn an toàn!
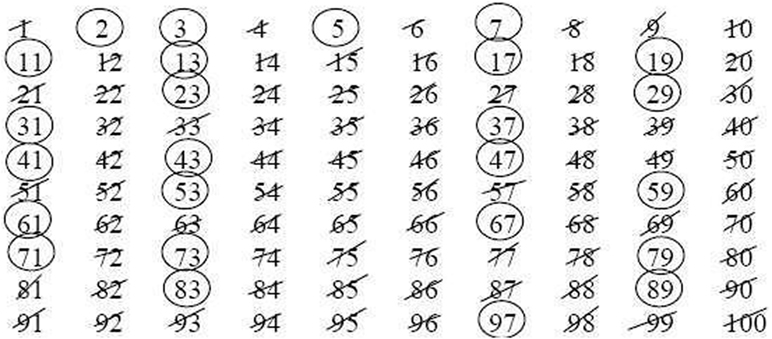
- Hình 2 – Rây của Eratosthenes.
- Số tổng hợp bị gạch bỏ và số nguyên tố được khoanh tròn.
TẦN SỐ CỦA CÁC SỐ NGUYÊN TỐ
Tần số của số nguyên tố là gì? Có bao nhiêu số nguyên tố, khoảng từ 1.000.000 đến 1.001.000 (một triệu và một triệu cộng với một nghìn) và bao nhiêu số từ 1.000.000.000 đến 1.000.001.000 (một tỷ và một tỷ cộng với một nghìn)? Chúng ta có thể ước tính số lượng các số nguyên tố từ một nghìn tỷ (1.000.000.000.000) đến một nghìn tỷ cộng với một nghìn không?
Các phép tính cho thấy rằng các số nguyên tố ngày càng trở nên hiếm hơn khi các số càng lớn. Nhưng liệu có thể phát biểu một định lý chính xác thể hiện chính xác mức độ hiếm của chúng không? Một định lý như vậy lần đầu tiên được phát biểu như một phỏng đoán
bởi nhà toán học vĩ đại Carl Friedrich Gauss vào năm 1793, ở tuổi 16. Nhà toán học thế kỷ 19 Bernhard Riemann ( Hình 1 ), người có ảnh hưởng đến việc nghiên cứu các số nguyên tố trong thời hiện đại hơn bất kỳ ai khác, đã phát triển thêm các công cụ cần thiết để đối phó với nó. Nhưng một bằng chứng chính thức của định lý chỉ được đưa ra vào năm 1896, một thế kỷ sau khi nó được phát biểu. Đáng ngạc nhiên là hai bằng chứng độc lập đã được cung cấp cùng năm bởi Jacques Hadamard người Pháp và de la Vallée-Poussin của Bỉ ( Hình 1 ). Điều thú vị là cả hai người đàn ông đều sinh ra vào khoảng thời gian Riemann qua đời. Định lý mà họ đã chứng minh được gọi là “ định lý số nguyên tố ” do tầm quan trọng của nó.
Công thức chính xác của định lý số nguyên tố, thậm chí nhiều hơn nữa chi tiết của chứng minh của nó, đòi hỏi toán học cao cấp mà chúng ta không thể thảo luận ở đây. Nhưng nói một cách không chính xác hơn, định lý số nguyên tố phát biểu rằng tần số của các số nguyên tố xung quanh x tỷ lệ nghịch với số chữ số trong x. Trong ví dụ trên, số lượng số nguyên tố trong “cửa sổ” có độ dài 1.000 khoảng một triệu (theo đó chúng tôi có nghĩa là khoảng từ một triệu đến một triệu và một nghìn) sẽ lớn hơn 50% so với số nguyên tố trong cùng “Cửa sổ” khoảng một tỷ (tỷ lệ là 9: 6, giống như tỷ lệ giữa số lượng số 0 trong một tỷ và một triệu) và nhiều gấp đôi so với số lượng số nguyên tố trong cùng một cửa sổ khoảng một nghìn tỷ (trong đó tỷ lệ của số số 0 là 12: 6). Thật vậy, các phép tính trên máy tính cho thấy có 75 số nguyên tố trong cửa sổ đầu tiên, 49 trong cửa sổ thứ hai và chỉ 37 trong cửa sổ thứ ba, từ một nghìn tỷ đến một nghìn tỷ cộng với một nghìn.
Thông tin tương tự có thể được minh họa dưới dạng đồ thị, được hiển thị bên dưới ( Hình 3 ). Bạn có thể thấy số π ( x ) của các số nguyên tố lên đến x thay đổi như thế nào trong phạm vi x ≤ 100 và một lần nữa đối với x ≤ 1.000. Lưu ý rằng bất cứ khi nào chúng ta gặp một số nguyên tố mới dọc theo trục x , đồ thị sẽ tăng 1, do đó đồ thị có dạng các bước ( Hình 3A ). Ở quy mô nhỏ, khó có thể phát hiện ra một mẫu trong biểu đồ. Khá dễ dàng để chứng minh rằng chúng ta có thể tìm thấy những khoảng lớn tùy ý trong đó không có số nguyên tố, nghĩa là những khoảng mà đồ thị không tăng lên. Mặt khác, một phỏng đoán nổi tiếng (xem bên dưới) nói rằng có vô số số nguyên tố sinh đôi
, nghĩa là, các cặp số nguyên tố có hiệu số giữa chúng là 2, sẽ chuyển thành “bước” có độ rộng 2 trong biểu đồ. Tuy nhiên, ở quy mô lớn hơn, biểu đồ trông mượt mà ( Hình 3B ). Đường cong trơn này được nhìn thấy trên diện rộng chứng tỏ định lý số nguyên tố.
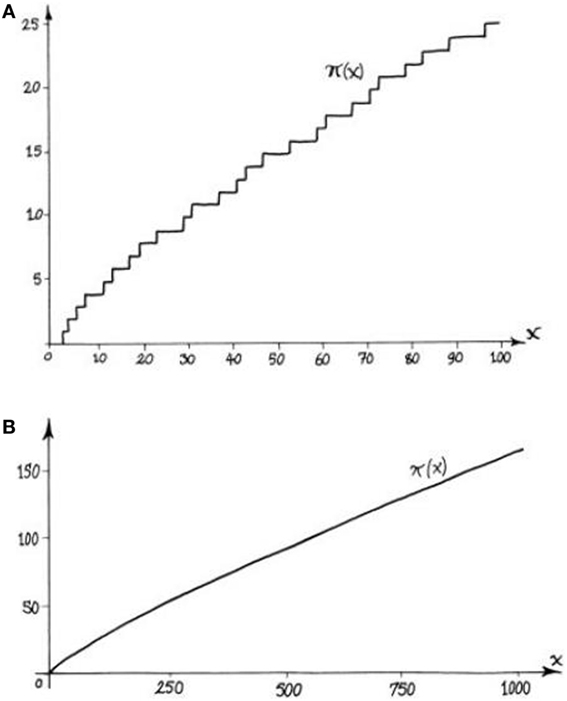
- Hình 3 – Tần số của các số nguyên tố.
- Đồ thị biểu diễn số π ( x ), số nguyên tố đến số x . Trong bảng A. x nằm trong khoảng từ 0 đến 100 và biểu đồ có dạng bậc. Trong bảng B. x nằm trong khoảng từ 0 đến 1.000, do đó tỷ lệ lớn hơn và đồ thị có vẻ mượt mà hơn nhiều.
Thực tế là một hiện tượng toán học dường như hoạt động ngẫu nhiên trong một tỷ lệ nhưng thể hiện tính đều đặn (trơn tru) ở một tỷ lệ khác / lớn hơn — một sự đều đặn ngày càng trở nên chính xác hơn khi quy mô lớn lên — không phải là mới đối với toán học. Các hệ thống xác suất, chẳng hạn như lật đồng xu, hoạt động theo cách này. Không thể dự đoán kết quả của một lần tung đồng xu, nhưng theo thời gian, nếu đồng xu không thiên vị, nó sẽ xuất hiện trong một nửa thời gian. Điều đáng ngạc nhiên là hệ thống số nguyên tố không có tính xác suất, nhưng nó vẫn hoạt động theo nhiều cách như thể nó được chọn ngẫu nhiên.
TÓM TẮT: AI MUỐN TRỞ THÀNH TRIỆU PHÚ?
Lý thuyết số, bao gồm nghiên cứu về các số nguyên tố, rất phong phú với các vấn đề chưa được giải quyết, được những bộ óc vĩ đại nhất giải quyết không thành công trong hàng trăm năm. Một vài trong số những bài toán mở đó là những phát biểu toán học chưa được chứng minh, nhưng chúng tôi rất tin tưởng vào tính đúng đắn của nó. Những định lý chưa được chứng minh như vậy được gọi là “phỏng đoán” hoặc “giả thuyết”. Chúng ta đã đề cập đến phỏng đoán liên quan đến sự tồn tại của vô hạn số nguyên tố sinh đôi — các cặp số nguyên tố cách nhau một khoảng là hai. Một giả thuyết nổi tiếng khác, được gọi là phỏng đoán Goldbach, phát biểu rằng mọi số chẵn có thể được viết dưới dạng tổng của hai số nguyên tố. Ví dụ: 16 = 13 + 3, 54 = 47 + 7. Nếu bạn chứng minh được bất kỳ điều gì trong số họ, bạn sẽ giành được danh vọng vĩnh cửu. 3
Có thể cho rằng vấn đề chưa được giải quyết nổi tiếng nhất trong toán học, giả thuyết của Riemann , được đề xuất bởi chính Bernhard Riemann, người đã được đề cập trước đó. Trong bài báo nghiên cứu duy nhất của Riemann về số nguyên tố, xuất bản năm 1859, Riemann đã nêu một giả thuyết dự đoán khoảng cách từ giá trị thực của π ( x ), số nguyên tố lên tới x , là giá trị gần đúng được đưa ra bởi định lý số nguyên tố. Nói cách khác, có thể nói gì về “thuật ngữ sai số” trong định lý số nguyên tố – sự khác biệt giữa đại lượng thực và công thức gợi ý? Clay Foundation đã đặt tên vấn đề này là một trong bảy vấn đề mà nó sẽ trả giải thưởng 1.000.000 đô la cho giải pháp! Nếu bạn không bị hấp dẫn cho đến nay, có thể giải thưởng này sẽ thúc đẩy bạn…
Tại sao nó lại quan trọng? Nó quan tâm đến ai? Các nhà toán học đánh giá vấn đề của họ trước hết bằng độ khó và vẻ đẹp nội tại của chúng. Các số nguyên tố đạt điểm cao trong cả hai tiêu chí này. Tuy nhiên, số nguyên tố cũng hữu ích một cách thiết thực. Nghiên cứu về số nguyên tố đã phát hiện ra một công dụng quan trọng trong mã hóa (khoa học mã hóa các thông điệp bí mật) trong vài thập kỷ qua. Chúng tôi đã đề cập trước đó về cuốn sách hư cấu của Carl Sagan, về một nền văn hóa ngoài Trái đất giao tiếp với loài người bằng cách sử dụng các số nguyên tố. Nhưng có một lĩnh vực “nóng” hơn nhiều, không phải là hư cấu, sử dụng các số nguyên tố cho mục đích dân sự hoặc quân sự; tức là, truyền được mã hóa. Khi chúng tôi rút tiền từ máy ATM, chúng tôi sử dụng thẻ ghi nợ và giao tiếp giữa chúng tôi và máy ATM được mã hóa. Giống như nhiều mã khác để mã hóa,